画像 三角比 求め方 中学 258589

 このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比（\\(\\sin, \\cos, \\tan\\)）を使った三角形の面積を求める方法はいくつか三角比の値から角度を求める問題が出てきたら、直角三角形の図をイメージしよう。 sinθ＝（高さ）/（斜辺） cosθ＝（底辺）/（斜辺） tanθ＝（高さ）/（底辺） の関係から、直角三角形をイメージすれば、角度θが求められるね。 そして θの範囲 にも注目しよう。 0°≦θ≦180° のときは、 座標平面の上半分 、 分度器 の範囲で考えるんだ。「隣辺比」 と呼ばれる解き方です。 右の図のように、 三角形abcと三角形adeで「ひとつの角（角a）が共通（重なっている）」とき、 面積の比はその共通角をはさむ2辺の積、 三角形abcの面積：三角形adeの面積＝5×9：2×4＝45：8 で求められるというものです。

力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

三角比 求め方 中学

三角比 求め方 中学- 今回の公式はなかなか証明が難しくて、理屈がはっきりとは理解しにくい部分もあったかもしれません。 なので、今回だけは 三角錐の体積は (三角錐の体積)= (底面積)× (高さ)× 、 表面積は面を構成している4つの三角形の面積を足し合わせれば良い のだと機械的に覚えてしまいましょう。 一方で、今回のような立体や図形の絡む問題では、展開図を持ち出す下の図の赤い三角形に着目して 、 ( )×250 = 180 ( ) × 2 50 = 180 より、 = 65 = 65 ・・・① 青い三角形に着目して、 x = 180 x = 180 ・・・② ①、②を見比べてみましょう。 = 65 = 65 ・・・① x = 180 x = 180 ・・・② ＋ ＝65 ＋ ＝ 65 を、②に代入できますね。 65x = 180 65 x = 180 x = 115° x = 115 °

三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典

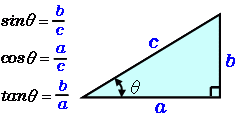
 1 1 2 = 3 1 2 3 = 6 1 2 3 4 = 10 のように順番に足していった和のことをいいます。 なぜ『三角』なのかというと、下の図がわかりやすいと思います。 『個数』を順番に並べていくと三角に配置されていくのです。 上記でわかるように ただ単純に足し算をしていくだけで答えの和が求められます。 しかしこの段数が増えていくにつれて和を求める計算 好きな言葉は「写像」。どうもこんにちは、ジャムです。 今回は先日紹介した外心と関連する話題です。 (記事はこちらから) jamjam1229hatenablogcom 先日の記事では詳しい外接円の半径の求め方は紹介していませんでしたが、 今回はそれについて紹介していきたいと思います！三角比ではルート2とルート3がよく出てくる。三角形は図のように直角の点が右下、斜辺が左上にくるようにします。 sin = 高さ／斜辺 cos = 底辺／斜辺 参考：ルート2からルート10までの小数 tan（タンジェント） tanはタンジェントと読み、高さ／底辺で求める。

まずは、三角形の面積を求めましょう。 参考： 三角比の面積公式と計算方法は？ いろんな場面での使い方を解説！ 面積の公式 を用いるため、 の値を求めます。 角Aに注目して、余弦定理を用いると ここから三角比の相互関係 を使って、 に変換すると だから これでようやく の値が求まったので、面積の公式 に当てはめていきましょう。 三角形の面積がこの問題のように，ほとんどの問題では三角比の値を求めるときに直角三角形による三角比の定義はそのまま使えません。余弦定理や正弦定理などを用いて求めることになります。 アドバイス 一般に，数学の問題を考える際に，定義をそのまま使いたいときには， 考えている状況が定義に三角比の考え方を拡張したものと考えてください。まずは直角三角形の角度、各辺の関係（三角比）を勉強しましょう。下記が参考になります。 三角比の定義は？1分でわかる定義、覚え方、表、直角三角形と単位円との関係 sin45度の値は？1分でわかる分数の値、求め方、cos45との違い、2分の

 面積比と線分比については、基礎編と、応用編があるにゃん 基礎編から読んで、次に応用編を読むのがオススメにゃん （基礎編）『数学三角形の辺と面積の比について、2つの考え方をサクッとまとめました中学数学 図形』三角形の辺の長さを求めるときの三角比の値 下の図の x の値を求めよ。 これを解こうとすると，sin45°，sin60°という三角比が出てきました。この見方は三角比から三角関数の学習にステップアップする上で非常に重要。 （同様に， 「sinθは斜辺の長さが1の直角三角形の高さを表している」と解釈できる。 ） あ，そうそう，例に挙げた θ ＝60°の直角三角形のように，角度と辺の比がわかって

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

 三角形EBC の面積は、14 × 10 ÷ 2 ＝ 70（cm²）で、三角形EBF の面積が（cm²）だから、 三角形FBC の面積は？ 70 — ＝ 50 （cm²）中学生からの質問（数学） や が出てくるのは，次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため，3つの角が30°，60°，90°である直角三角形と，45°，45°，90°である直角三角形の3辺の長さには，それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°，60°，90°の三角比は，直角三角形の辺の比を表します。 長さがわからない辺があるので，まずは三平方の定理を利用してすべての辺の長さを求めましょう。 次に，定義に従って三角比の値をそれぞれ求めます。 今回の問題では が左下にあるので簡単に求められます。

三角関数 度 高精度計算サイト

三角関数のsin Cos Tanとは 図解ですぐわかる 超重要な公式と練習問題も 高校生向け受験応援メディア 受験のミカタ

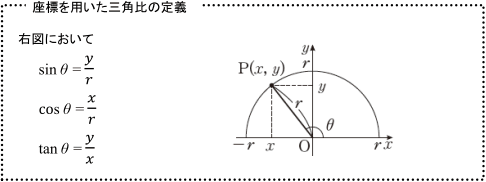
三角比を求められるようにしておきましょう。 仰角とは物を見上げたときの視線の方向と， 水平方向とのなす角で，俯角とは物を見下ろした ときの視線の方向と，水平方向とのなす角です。 15°, 25° の三角比は次ページの三角比の表を利用 15° しましょう。 右図において， sin𝜃= , cos𝜃また，三平方の定理から， ∗三平方 きの点P の座標を求め，三角比を計算 せよ。 (1) r =1のとき P( , ) sin1 = cos1 = tan1 = (2) r =2のとき P( , ) sin1 = cos1 = tan1 = 高知工科大学基礎数学シリーズ3 「三角関数」(改訂版) −7 − < 鈍角の三角比2 > 図1の場合 sinθ= Y r , cosθ= X r , tanθ= Y X である。 問1 三角形の角度を求める時 sin cos tan などを求めて三角比の表を見て角度を求めるといった方法がありますが、その表を使わないで角度を求める方法ってないですか？ 三角形の辺すべての長さは分かっているというのが条件です。 詳しく

高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット

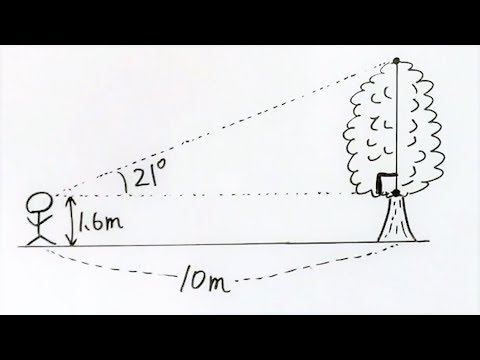
三角比の応用 木の高さを求める 一夜漬け高校数学110 Youtube

 このページは、このような人に向けた内容となっています \(\sin, \cos, \tan\)が何のことなのかイマイチ分からない \(\sin, \cos, \tan\)の求め方がわからない \(0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}, 90^{\circ}\)の三角比（\(\sin, \cos, \tan\)）が覚えられない 三角比を学ぶ上で必ずマスターしなければいけないこれが中学入試に出た図形問題！ 公式、法則、受験算数の極意 中学受験算数分野別68項目へ 中学入試算数、よく出る問題はこれ！ 1分で解ける算数 今年、15年に出た中学入試算数問題！ 図で解く算数 紙も鉛筆も使わないで解く算数こちらの記事で説明したように、 三角形の面積比は「（底辺の比）×（高さの比）」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。

三角関数の公式 Sin Cos Tan と覚え方

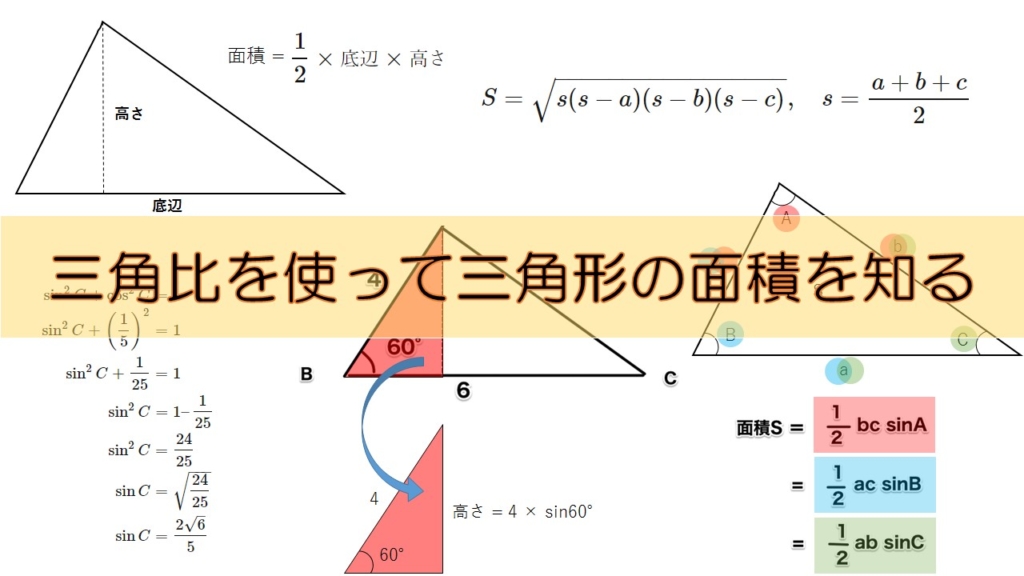
高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

このとき、「底辺×高さ」が同じ大きさであれば、三角形の面積はどちらも同じ面積になるということがおわかりでしょうか。 以上のことから、三角形の面積比を考える場合、「 （底辺の比）×（高さの比）＝面積の比 」となることがわかります。 まとめ直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか？ 三角形の比についてよくわからない方は、三角比（30°,45°,60°） をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角三角形に描いてある水色の線を見てく（※三角形agpと三角形inrは合同ですから、ap＝riです。） がわかり、ap：pq：or：ri＝3：1：5：3 が求められます。 （3）は、 について面積比を求めるのですから、（2）が正解できれば容易です。 三角形pqm：三角形rin：三角形pik＝1×1：3×3：9×9＝1：9：81 なので、

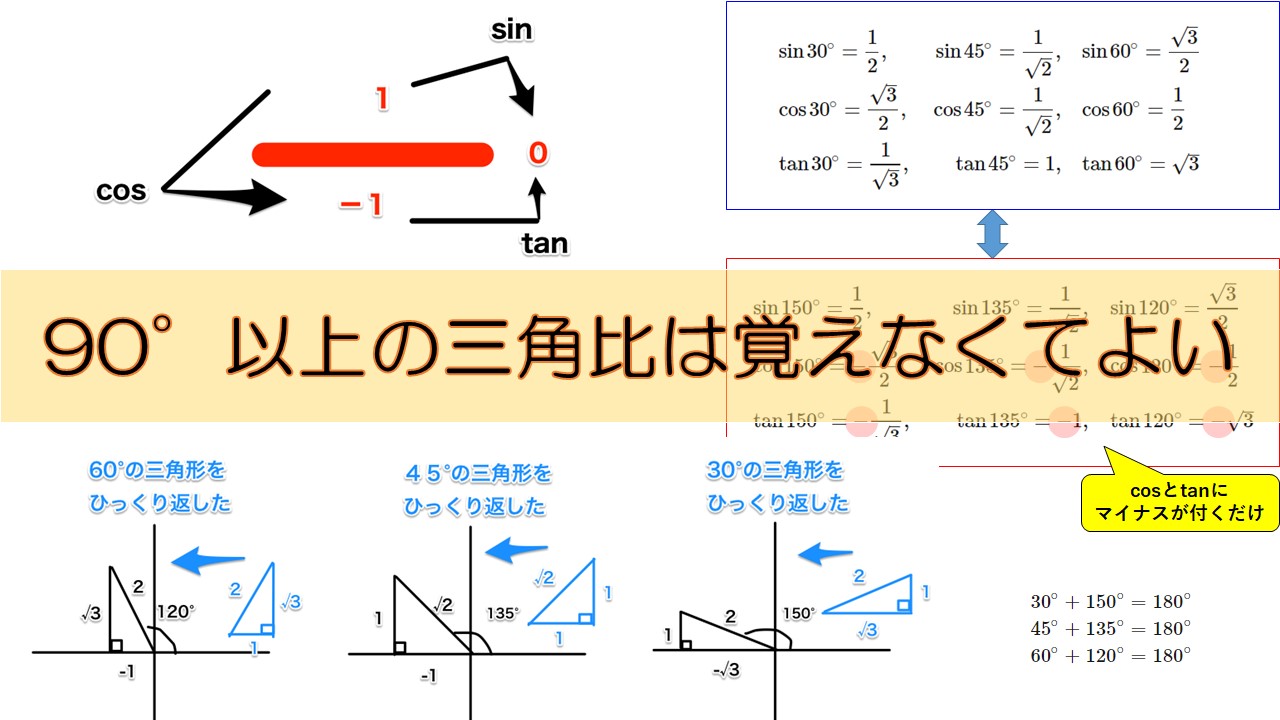
高校数学 三角比 三角比の拡張 90 より大きいsin Cos Tanは簡単に求めることができる 数学の面白いこと 役に立つことをまとめたサイト

三角関数です Y切片の求め方が分かりません Clear

だから、 外角の大きさ ＝ ★ ってこと！ ホント・・？？じゃあ、この三角形の外角を求めてみよう！ 外角の求め方① 40°75°∠x＝180° → ∠x＝65° 三角形の1つの外角 → 赤色の外角 のこと; 中学数学ではわからなくても大丈夫！ 先がとんがった立体の体積は最後に3でわる っておぼえておこう。 まとめ：三角錐の体積の求め方の公式は3ステップ！ 三角錐の体積の求め方をマスターしたね。 ようは、 底面積をだして、 高さをかけて、

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

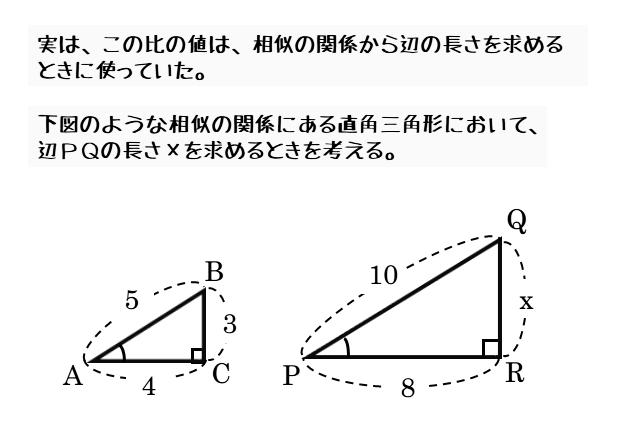
図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん

 三角形の面積を求めるにあたって, 三角形の3辺の長さが分かっていれば, 面積は必ず求められるという事実を ご紹介いたしましょう。まず, 三角形の高さが三角形の内部にできる場合を考えます。下の図で, 3辺の長さは, 7, 5, 3である。 長さ7の部分が底辺になっていると考えてください。 そ 三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。 S 2 = a b 2 真ん中の 正方形の面積 S 3 は、 S 3 = c 2 大きな正方形 S 1 は、三角形 S 2 4つと 真ん中の正方形 S 3 との合計でも求めることが出来ます。 S 1 = 4 S 2 S 3 ( a b) 2 = 4 × a b 2 c 2 a 2 2 a b b 2 = 2 a b c 2 ∴ a 2 b 2 = c 2 よって、ピタゴラゴラスの定理 a 2 b 2 = c 2 が導き出されました。

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

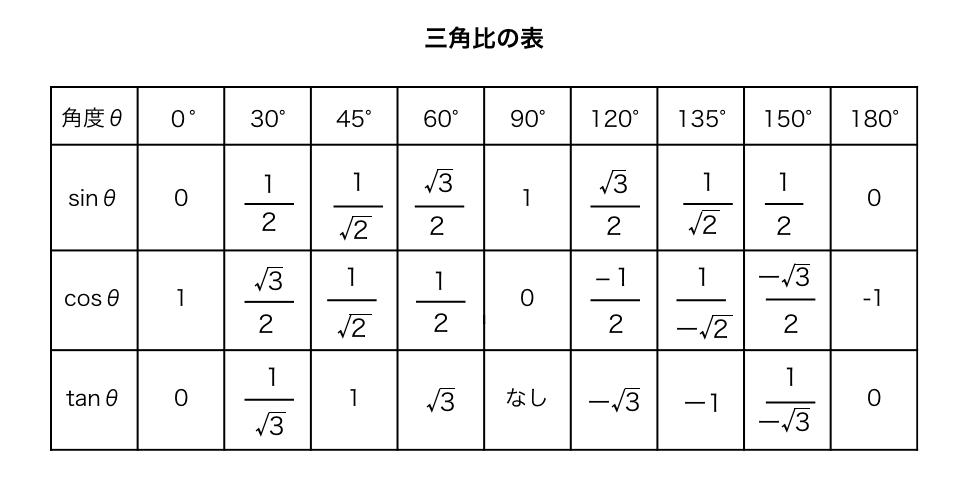
三角関数の公式 Sin Cos Tan と覚え方

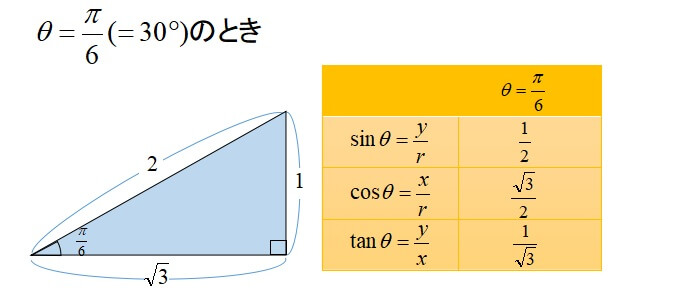
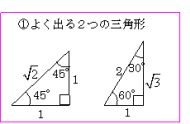
≪三角比の値の求め方≫ sinθ，cosθ，tanθの値は，次の「よく出る2つの三角形」と「sinθ，cosθ，tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値（角度）を見て，「よく出る2つの三角形」のうち，当てはまる三角形をかき出す。 算数｢平面図形と比（1）｣中学受験 中学受験 受験算数でも頻出の「平面図形と比」を取り上げます。 図形問題は、図形や数値など、問題から得られる「見えている情報」から、いかに「見えていない情報」を引き出すかがカギ。 それには、図形に 求め方 \(~\cos{18^{\circ}}~\) の求め方 次の図のような \(~AB=AC=1,\angle{A}=36°~\) の \(~\triangle ABC~\) を考える。 \(~\angle{B}~\) の二等分線と \(~AC~\) の交点を \(~D~\) とする。 このとき、 \(~\triangle BCD~\) や \(~\triangle DAB~\) も二等辺三角形となるので、 \(~BC=BD=AD=1~\)である。

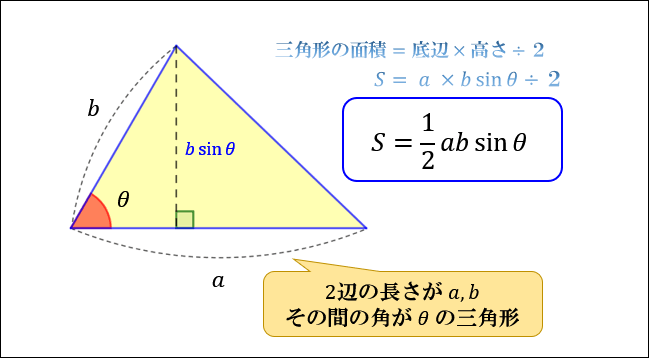
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

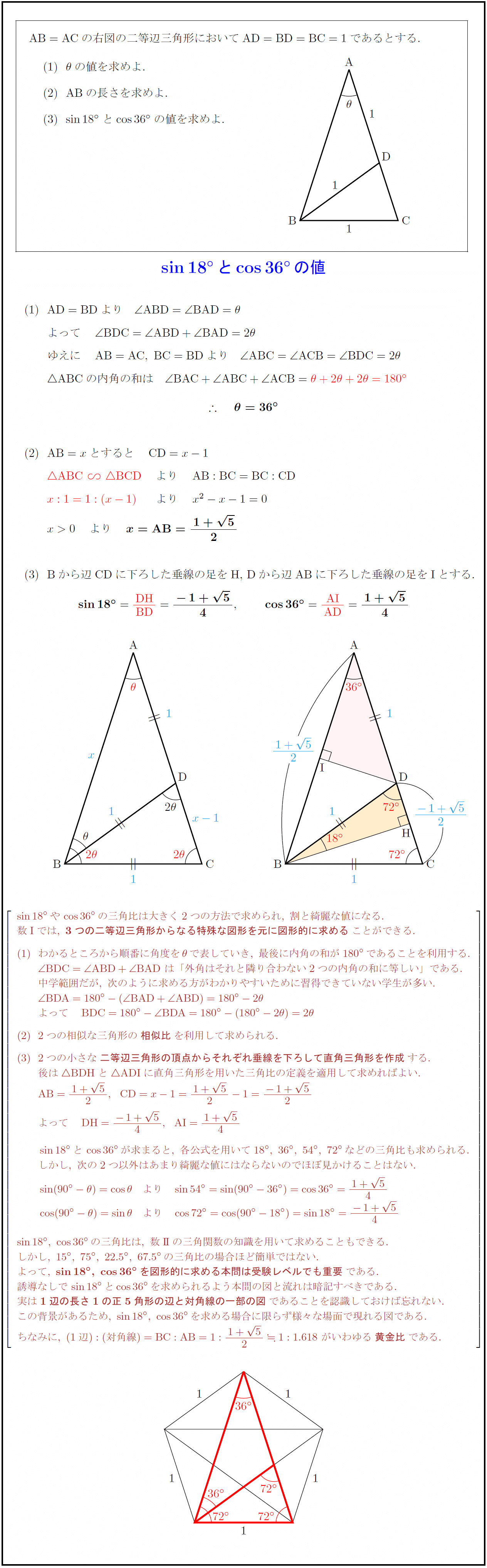
高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月

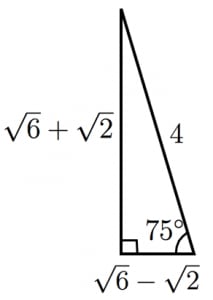
解答 左の直角三角形は、正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 よって、下の図のように長さが決まります。 x= 3√3 x = 3 3 です。 右の直角三角形は、正方形を半分にした直角二等辺三角形です。 3 3 辺の比は暗記で、 11√2 1 1 2 です。 よって、下の図のように長さが決まります。 y= 3√6 y = 3 6 です。

力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

高校数学 数 ７６ 三角比 基本編 Youtube

90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座

数i 基本的な三角比の値

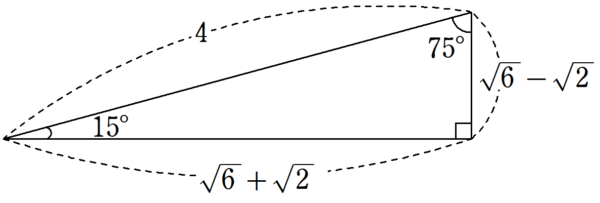
15 の三角比 Fukusukeの数学めも

覚えておくと便利な三角比の値 高校数学の美しい物語

三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

高2 数学ii B 三角比 三角関数公式まとめ 高校生 数学のノート Clear

数i 基本的な三角比の値

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角関数表 Pukiwiki

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

高校数学 数 ７９ 三角比 暗記編 Youtube

三角比の表を見て三角形の角度を求める問題 数学i By ふぇるまー マナペディア

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

高校数学 90 を超える三角比2 135 150 映像授業のtry It トライイット

Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

3

力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

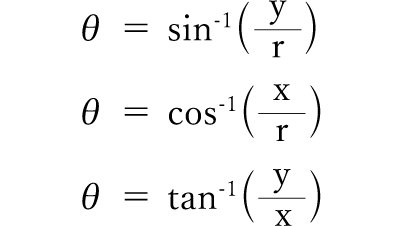
三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習

わかりやすい三角比と基本公式 Irohabook

三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

タンジェントとは何か 中学生でも分かる三角関数の基礎

三角関数のsin Cos Tanとは 図解ですぐわかる 超重要な公式と練習問題も 高校生向け受験応援メディア 受験のミカタ

三角比画像の傾斜角の大きさの求め方を教えてください 中学レベルの数学し Yahoo 知恵袋

数 三角比 Sinbの求め方を教えていただきたいです 画像見づらくてすみません Clear

三角比を使ってビルの高さを求める 数学i By はっちゃん マナペディア

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

1

高校数学 三平方の定理による三角関数の計算 ２ 映像授業のtry It トライイット

高校数学 三角比を利用した長さの求め方2 例題編 映像授業のtry It トライイット

三角関数表 Pukiwiki

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典

下の図において X Yの値を 三角比の表を用いて求めよ ただし 少数 高校 教えて Goo

高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

3

中学数学 覚えておくと得する三角比 ジャムと愉快な仲間たち 0名

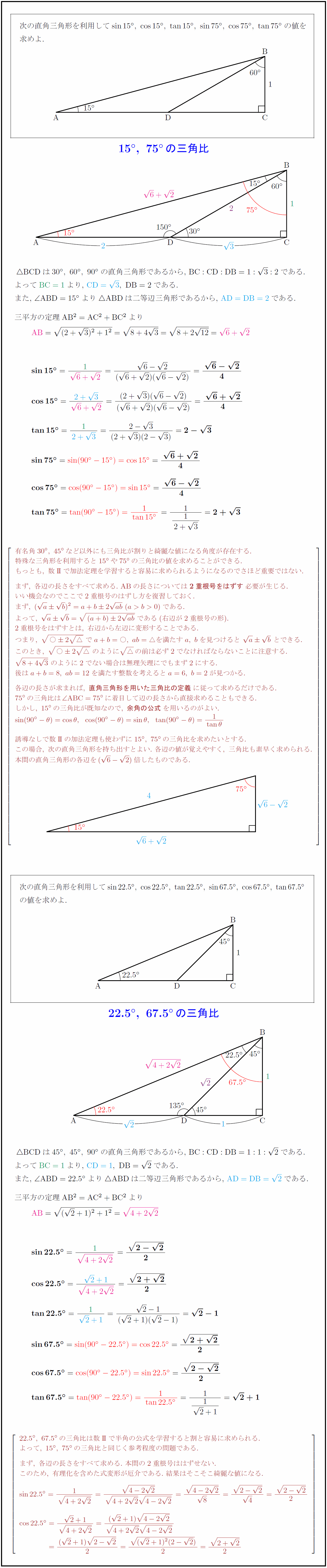
高校数学 15 75 22 5 67 5 の三角比の値の図形的な求め方 受験の月

高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月

力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト

グラフの周期の求め方を教えてください Clear

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

Sin15 Cos15 Tan15 を簡単に求める 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

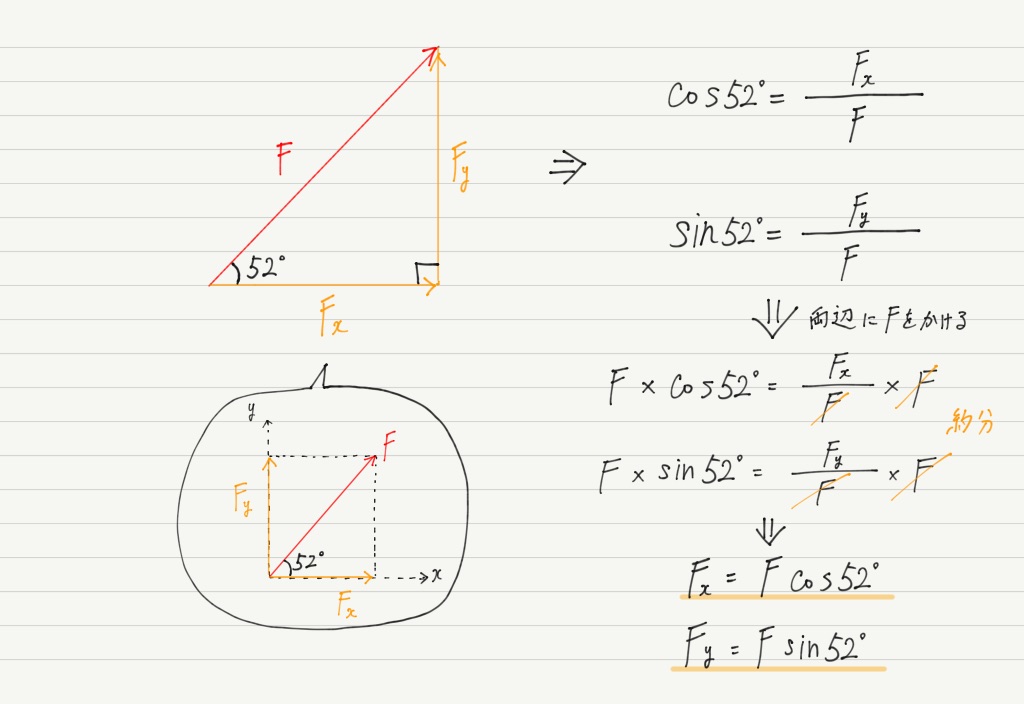
力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

正確な角度の測定 割り付け

数i 基本的な三角比の値

高校数学 三角比を利用した長さの求め方2 練習編 映像授業のtry It トライイット

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

わかりやすい三角比と基本公式 Irohabook

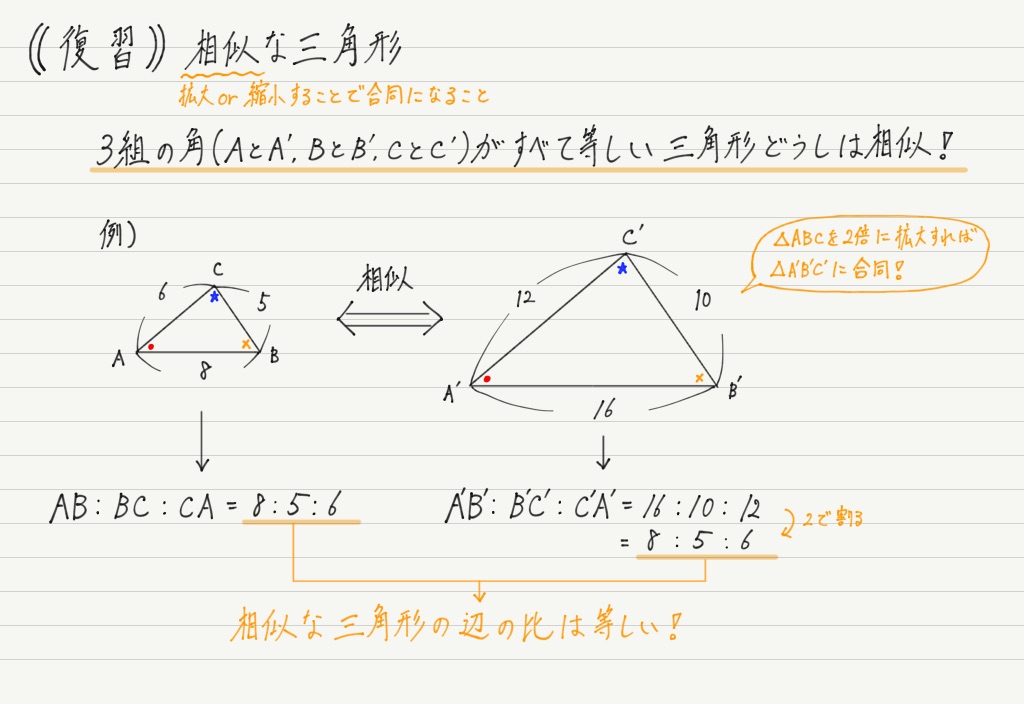
三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

黄金三角形による18 シリーズの三角比 おいしい数学

三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ

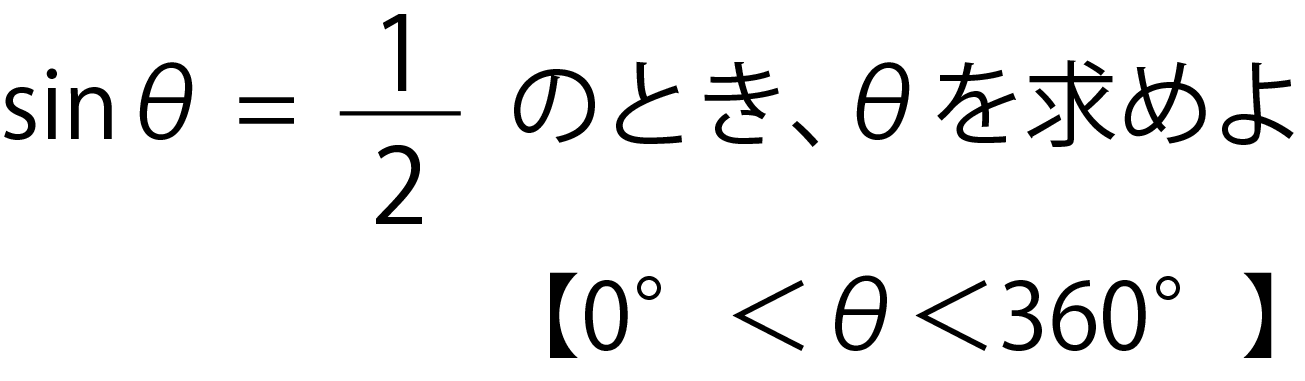
三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

高校数学 超重要 30 と60 の三角比 映像授業のtry It トライイット

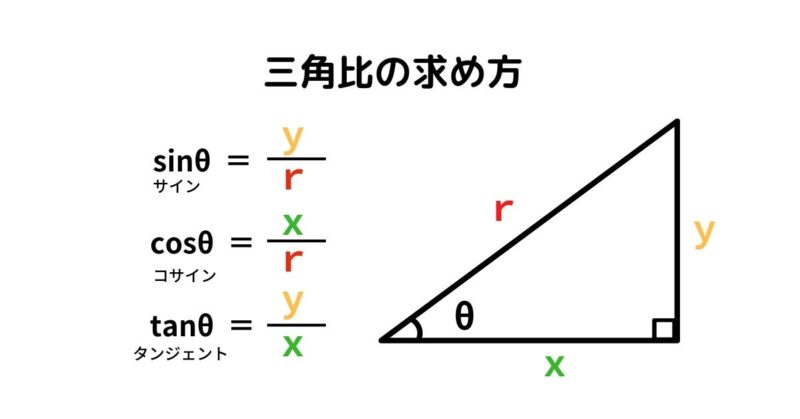
三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

わかりやすい三角比と基本公式 Irohabook

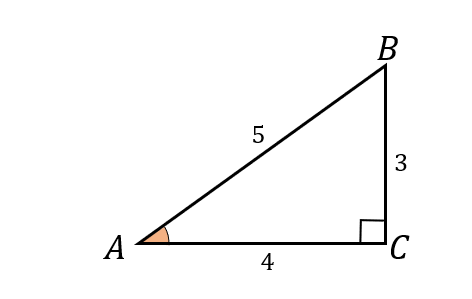
三角比の値の求め方 数学苦手な人に向けて基本をイチから解説していくぞ 数スタ

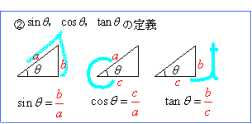
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

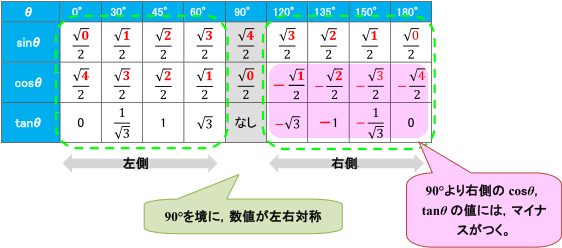
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

三角関数表 Pukiwiki

48s96ub7b0z5f Net Sankakuhi Sougo

三角比の表と面積公式 正弦定理 余弦定理を一記事で解説

中学数学 覚えておくと得する三角比 ジャムと愉快な仲間たち 0名

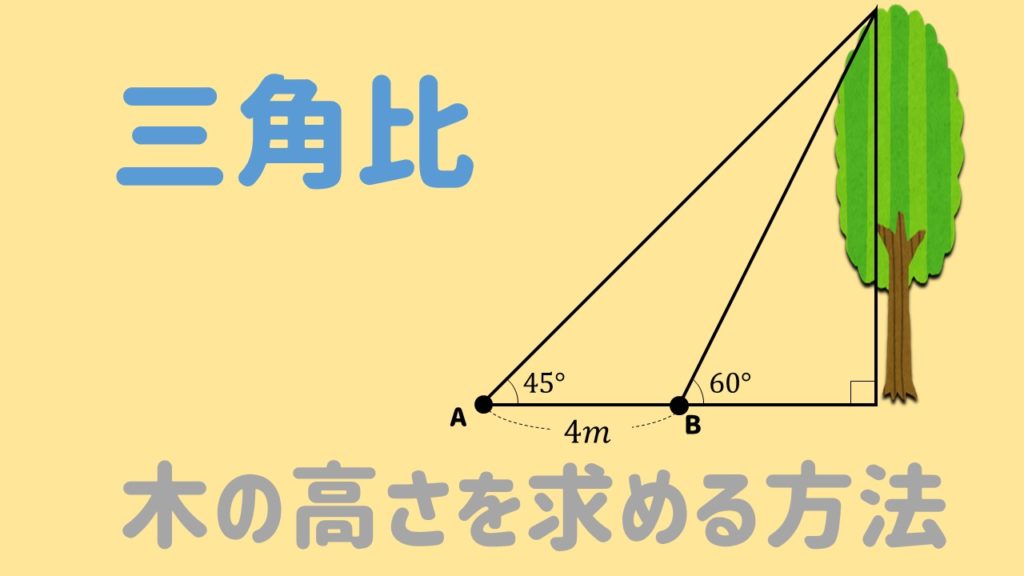
高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

高校数学 180 8の三角比 映像授業のtry It トライイット

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

三角比 30 45 60 もう一度やり直しの算数 数学

三角比で辺の長さを表す問題がいまいちよく分かりません 求め方のポイントなど Yahoo 知恵袋

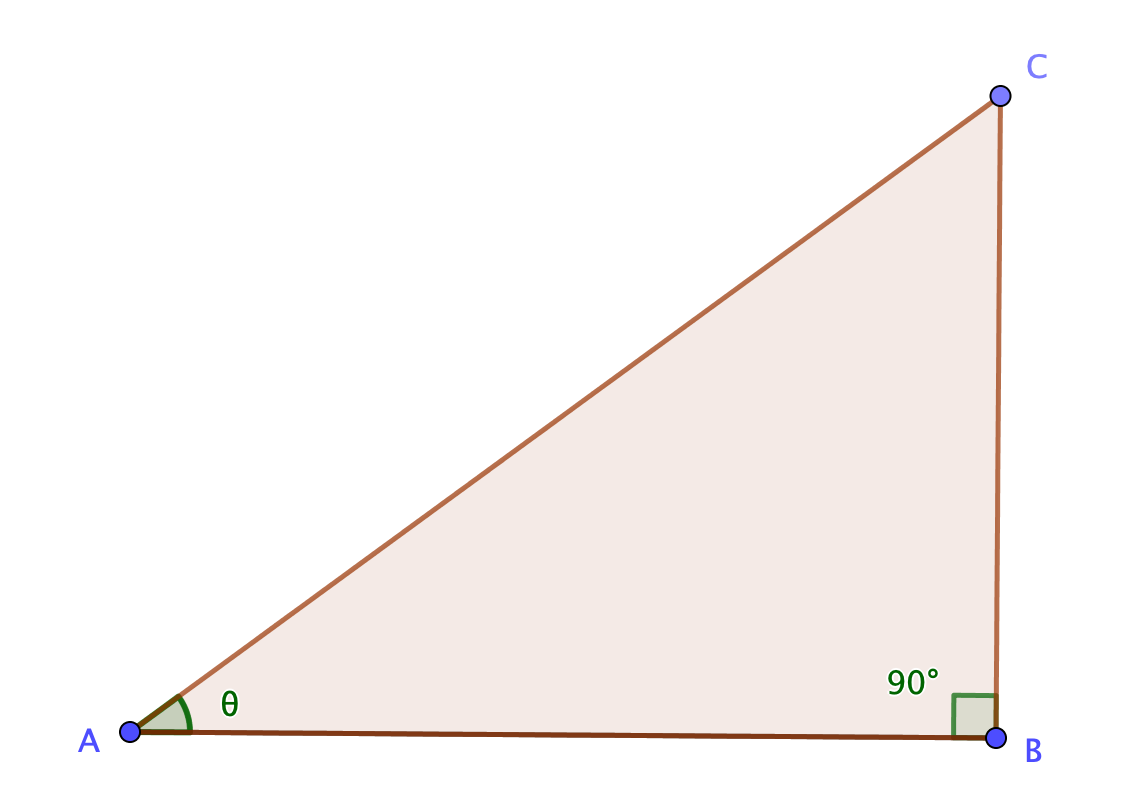
中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック

わかりやすい三角比と基本公式 Irohabook

単位円を用いてサイン コサインを導きます 一歩一歩ぐんぐんブログ

タンジェントとは何か 中学生でも分かる三角関数の基礎

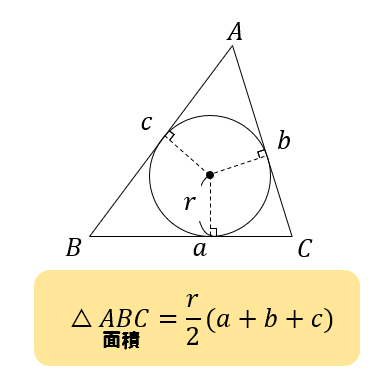
三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ